Text Box: NEXT  

                                                                         

Text Box: PREVIOUS

 

2.4: Denavit-Hartenberg parameters

 

In order to find a transformation from tool tip to the base of a manipulator, we have to define link frames and to derive a systematical technique, which allows to describe the kinematics of a robot with degrees of freedom in a unique way. A set of parameter will turn out to be sufficient for that purpose.

Figure 2.7: Links of a kinematics chain

Figure 2.7 presents the first links of a kinematics chain. The base and each link of the chain is assigned to a specific frame , which is fixed to the link. So the position and orientation of a link frame changes with respect to a neighboring link frame according to the motion of their connecting joint. Therefore coordinate frame can be described from its precedent link frame by means of a homogeneous transformation. This homogeneous transformation includes the joint angle (for rotary joints) or the joint offset (for prismatic joints).

Finally the tool frame can be transformed to the base frame by multiplication of all the link transformations through the kinematic chain. So in order to transform any position/orientation relative to the tool frame (e.g. by sensorics attached there) towards the manipulators base frame (e.g. where it is fixed to the floor), the sorted sequence of homogeneous transformations from tip to toe via has to be processed. The remaining task is to set up all the homogeneous transformation matrices for a particular type of kinematic chain, considering geometrical attributes of link arrangements and types of joints.

Figure 2.8: Assignment of DH-parameters

Figure 2.8 shows a detail of a kinematic chain, where two links are connected via a rotary joint. It is used to show, how invariant parameters are obtained which describe a link.

The axes of rotation for link and are extended towards straight lines , , which in general are warped with respect to each others. The straight lines and have a common normal line , which is perpendicular to both of them. The point of intersection between straight line and normal line is defined as origin of link frame . Further on, the base vector is defined as extension of the normal line, whereas the base vector of this link frame is assumed to be matching the straight line and thereby describing the axis of rotation for link . Now given the vectors and , the remaining base vector of this frame $\mbox{\boldmath$y$}_i$is chosen appropriately in order to create a right-hand coordinate frame.

Let us assume that the same operation has already been carried out for the precedent links. In this case, coordinate frame is determined with its origin located on straight line .

We are now able to derive some necessary parameters for link description. Parameter is already introduced, whereas the second characteristic parameter is defined here as distance between origin of frame and the intersection of normal line (but this time) with straight line .

Obviously the origin of frame is located in the plane, which is stretched out by the pair of joint rotation vectors and. One more characteristic link parameter is the angle, which occurs between both joint rotation vector and.

For link , the rotation of its rigid body (with respect to its rigid body ) is given by the rotation angle . In other words, angle is located between -axis and -axis.

For revolute joints, joint parameters und are constant. They depend on joint design only and do not include any joint motion. The only variant parameter for revolute joints is the angle, which describes variable joint positions.

The situation is different for prismatic joints. Here parameter becomes variable and describes translational joint positions, whereas parameters und depend on joint design only.

 

However, in principle prismatic and revolute joints can be completely described with just 4 parameters:

Length of normal line

Angle between and

Length of line

Angle between and

A homogeneous transformation mapping frame towards via the actual link, can be derived now from the following geometrical transformations via the link under consideration:

1.

Rotation around with angle

2.

Translation along with displacement

3.

Translation along with displacement

4.

Rotation around with angle





 

or, in a more formal description with the help of homogeneous transformation matrices for each of the 4 actions mentioned above:

 


 

 

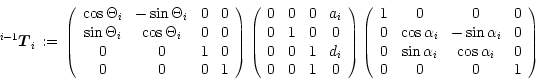
, which leads to the following general description of transformations via prismatic or revolute joints:

 

(2.11)


 

Apparently homogeneous link transformations become especially simple, if the angular parameter is set to some specific values, which are multiplicities of . As parameter is always constant, no matter whether a prismatic or a revolute joint is considered, simplifying the link transformation can be done through joint construction. From the physical viewpoint, becomes a multiplicity of, if neighboring axis are in parallel or perpendicular to each others.

In fact, most of the industrial robots are designed according to these considerations. Observing this construction rule does in no way restrict any practical demands on the robot. Thereby some necessary calculations are facilitated for the robot controller, for example transformations from cartesian task descriptions to joint motion interpolation, and vice versa.

One more practical demand for robot design has to be mentioned here:

There is one posture of the robot arm (of its open kinematic chain), where all the joints are in 'zero' position. This posture itself is called the arms' zero position. Usually it is a reference position for measurement of joint positions by internal sensorics. Therefore the posture should be physically accessible for the robot.

 

Example

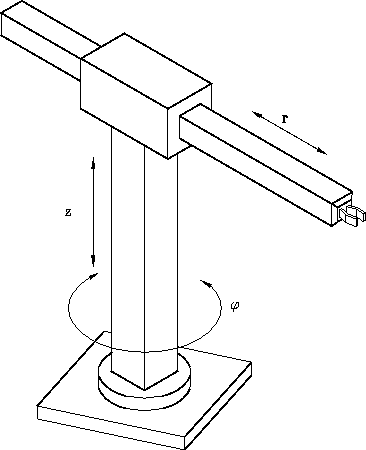
Consider the classical cylindrical robot, which means this type of robot moves in radial, angular and vertical components due to the special arrangement of robot joints.
There is a translational joint for radial motion, a revolute joint for angular motion and another translational joint for vertical motion available.
This special arrangement gives 3 cylindrical degrees of freedom.
The robot is presented in figure 3.3. Note that the robot has a minimum radial component of value $A$.

 

 

Figure 3.3: The classical cylindrical robot
\begin{figure} \begin{center} \epsfig {file=PICS/stanford.eps,width=8.5cm}\end{center}\end{figure}

 





Task:

Find the forward transformation of the cylindrical robot via Denavit-Hartenberg frame assignments, thus relating joint positions $r(t), \varphi(t), z(t)$ to cartesian positions in the robots base frame $x_0, y_0, z_0$.





Solution:

According to the previously introduced frame assignment concept we define 4 different frames for the given cylindrical robot:

 

 

Figure 3.4: Frame assignment for the cylindrical robot
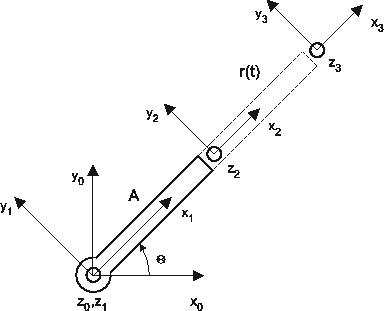\begin{figure} \begin{center} \epsfig {file=PICS/diag.eps,width=8.5cm}\end{center}\end{figure}

 

Transformation between these frames is based upon the general transformation description given above.
The individual transformations between neighboring frames are as follows:
 

 

I.

$a_1 = 0 \;\; , \;\; \alpha_1 = 0 \;\; , \;\; d_1 = 0 \;\, , \;\; \Theta_1 = \varphi (t)$
 


 

 

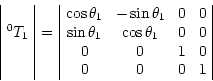
\begin{displaymath} \begin{array}{\vert l\vert c\vert cccc\vert} & & \cos \thet... ...0 \\ & & 0 & 0 & 1 & 0 \\ & & 0 & 0 & 0 & 1 \\ \end{array}\end{displaymath}


 

 

 

II.

$a_2 = 0 \;\; , \;\; \alpha_2 = 90^\circ \;\; , \;\; d_2 = z(t) \;\; , \;\; \Theta_2 = 90^\circ$
 


 

 

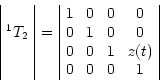
\begin{displaymath} \begin{array}{\vert l\vert c\vert cccc\vert} & & 1 & 0 & 0 ... ...\ & & 0 & 0 & 1 & z(t) \\ & & 0 & 0 & 0 & 1 \\ \end{array}\end{displaymath}


 

 

 

III.

$a_3 = 0 \;\; , \;\; \alpha_3 = 0 \;\; , \;\; d_3 = r(t) \;\; , \;\; \Theta_3 = 0$
 


 

 

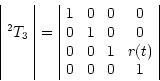
\begin{displaymath} \begin{array}{\vert l\vert c\vert cccc\vert c\vert r\vert} ... ...\ & & 0 & 0 & 1 & r(t) \\ & & 0 & 0 & 0 & 1 \\ \end{array}\end{displaymath}


 

 

 

Thus the resulting transformation between tool frame $x_3, y_3, z_3$ and the base frame $x_0, y_0, z_0$ is given by ${}^0\mbox{\boldmath$T$}_3$:


 

 

\begin{displaymath} {}^0\mbox{\boldmath$T$}_3 \; = \; {}^0\mbox{\boldmath$T$}_1 \; {}^1\mbox{\boldmath$T$}_2 \; {}^2\mbox{\boldmath$T$}_3 \end{displaymath}


 

 

The complete notation is:


 

 

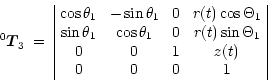
\begin{displaymath} {}^0\mbox{\boldmath$T$}_3 \; = \; \begin{array}{\vert cccc\v... ...heta_1 \\ 0 & 0 & 1 & z(t) \\ 0 & 0 & 0 & 1 \\ \end{array}\end{displaymath}


 

 

Observing the motion of frame $x_3, y_3, z_3$ itself in cartesian space, set $x_3 = 0 \; , \; y_3 = 0 \; , \; z_3 = 0$.
 

This frame moves in 3D space with the following dependencies on joint motions $\Theta_1(t), r(t), z(t)$:

 

 

\begin{eqnarray*} x_0 (t) & = & [A+r(t)] \cos \Theta_1 \\ y_0 (t) & = & [A+r(t)] \sin \Theta_1 \\ z_0 (t) & = & d_z(t) \\ \end{eqnarray*}
 

 

 

Back to top