	Sign In Sign-Up

2.3: Homogeneous transformations

We return to the description of general locations (position and orientation) in 3D space. As a result of our previous considerations we have found it sufficient in order to describe locations, that we apply a position vector to describe translations with respect to a reference frame, and an orientation matrix to describe rotations.

Figure 2.5 assumes, that the location of a cube is available via position vector and orientation matrix. Position of the corner opposite to the bodies frame is known relative to the body frame via .

Figure 2.5: Body position in base frame

With respect to the universal frame , the position of is:

The given result is achieved by simple addition of vectors and .

This procedure can be easily extended to describe more complex relations between frames.

Figure 2.6: Series of homogeneous transformations

Figure 2.6 shows the derivation of a position vector , where position is known relative to frame . All the frames are related via a position offset between their origins, which is described by vectors and .

Alternatively it can be calculated:

This equation can be reduced in a very handsome way by introducing homogenous coordinates and transformation.

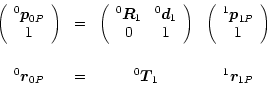
A closer look shows the benefits of this notation:

Position vector has been extended here with a forth coordinate of constant value .

This enlarged presentation of a position is called homogeneous coordinates notation. The homogeneous transformation matrix includes all necessary information about the position and orientation of a reference frame with respect to another frame.

In homogeneous representation the previous equation becomes:

Obviously the mapping of frame towards frame is accomplished by a simple multiplication of individual transformations.

Example

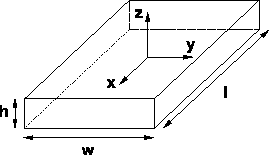
Consider the homogeneous rectangular beam of mass , length , width and height , as presented in figure 5.3.

**Figure 5.3:** Homogeneous rectangular beam
$\begin{figure} \begin{center} \unitlength1.0cm \epsfig {file=PICS/balken.ps,width=6.00cm}\end{center}\end{figure}$

There is a homogeneous distribution of mass density in the beam, which means:

$\begin{displaymath} \rho \; = \; \frac{m}{l \; w \; h} \end{displaymath}$

As shown, this define a body frame in the center of mass of the beam, and arrange the coordinate axes according to the principal axes of the beam.

To find the moments of inertia and set up the corresponding inertia tensor follow the rules presented above. The moment of inertia with respect to the -axis of the frame becomes:

$\begin{displaymath} I_{xx} \; = \; \int_V \frac{m}{l \; w \; h} \; (y^2 + z^2) \... ...{-\frac{l}{2}}^{\frac{l}{2}} \; (y^2 + z^2) \; dx \; dy \; dz \end{displaymath}$

This leads to:

$\begin{displaymath} I_{xx} \; = \; \frac{m}{l \; w \; h} \left( \frac{1}{12} (l... ... h^3) \right) \;\; = \;\; \frac{m}{12} \; (w^2 + h^2) \;\;\; , \end{displaymath}$

The same calculation applies for the moments of inertia $I_{yy}$ und $I_{zz}$ .

Finally let us consider moments of deviation, for example in $I_{xy}$ and generalize the result for all other moments of deviation.

$\begin{displaymath} I_{xy} \; = \; - \; \int_V \; \frac{m}{l \; w \; h} \; (xy) ... ... \int_{-\frac{l}{2}}^{\frac{l}{2}} \; (x y) \; dx \; dy \; dz \end{displaymath}$

conclude:

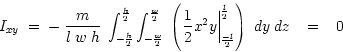
$\begin{displaymath} I_{xy} \; = \; - \; \frac{m}{l \; w \; h} \; \int_{-\frac{h}... ...c{- l}{2}}^{\frac{l}{2}} \right) \; dy \; dz \;\;\; = \;\;\; 0 \end{displaymath}$

The same result applies for all other moments of deviation.

Now can set up the inertia tensor:

$\begin{displaymath} {\cal I} \; = \; \left[ \begin{array}{ccc} \frac{m}{12} (w^2... ... & 0 \\ 0 & 0 & \frac{m}{12} (w^2 + h^2) \end{array}\right] \end{displaymath}$