|
|
|
![]()
![]()
2.1: Position and Orientation
Introduction of position
The position of a point (or the origin of one frame relative to another) is given by a vector p=px, py, pz. In general we use a right-hand Cartesian coordinate system with 3 mutually orthogonal unit vectors to define any reference system for positions and orientations in space.
To describe the position and orientation of a body in space, a fixed reference coordinate system is attached to it. It is called the base frame system of the body and can be referenced to any other frame system.
The bodies' own base frame system can be assign to any arbitrary location. However, for convenience the origin of this base system is usually chosen to be in its geometrical center, or in its center of gravity or in one of the bodies' corners.
In figure 2.1, the corner of a cube-type body is defined as origin of the attached base frame. The orientation of the unit vectors is in parallel with the neighboring edges of the body.
|
|
|
Figure 2.1: Right-hand Cartesian base system |
In a first step, let assume the position of a body location
![]() with
respect to the own base frame of the body.
with
respect to the own base frame of the body.
The position of a location in space is definitively defined by a
![]() position
vector
position
vector
![]()
|
|
(2.1) |
For example, the position of the cubes' origin
![]() is
given by:
is
given by:
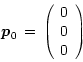
,whereas the position of its opposite corner
![]() is:
is:
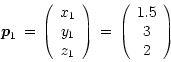
It is obvious, that values of vector elements are dependent on the location (position and orientation) of the reference frame. So whenever more than one reference frame is involved in a problem description, it is urgently necessary to include the name of the reference frame into the notation of position vectors itself. In general, we add a leading superscript to a position vector (or rotation matrix) in order to refer it to a particular coordinate frame.
The position vector ![]() of
a point with respect to frame
of
a point with respect to frame ![]() is
therefore:
is
therefore:
|
|
(2.2) |
In a second step, we start to describe the position and orientation of a body
in space with respect to another frame ![]() (e.g.
a universal frame) with the help of the bodies' frame
(e.g.
a universal frame) with the help of the bodies' frame
![]() .
.
Figure
2.2 shows, how
the position of body frame ![]() is
related to the universal frame
is
related to the universal frame ![]() .
A similar procedure is necessary to describe its orientation with respect to the
predefined universal orientations.
.
A similar procedure is necessary to describe its orientation with respect to the
predefined universal orientations.
|
|
|
Figure 2.2: Position of a body in 3D space |
.
Introduction of Orientation
The orientation of a body or a frame can be defined by 3 angles, or rather by a sequence of 3 rotations. Using axes fixed in space we can define roll, pitch and yaw angles about x, y and z respectively.
To describe the orientation of a body frame
![]() with
respect to a universal base frame
with
respect to a universal base frame ![]() ,
its three orthogonal unit vectors are considered, which are:
,
its three orthogonal unit vectors are considered, which are:
for ![]() -direction
of frame
-direction
of frame ![]() :
:
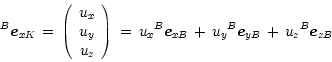
for ![]() -direction
of frame
-direction
of frame ![]() :
:
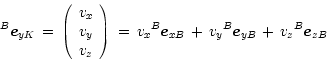
for ![]() -direction
of frame
-direction
of frame ![]() :
:
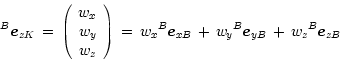
These vectors are combined towards a matrix
![]() :
:
|
|
(2.3) |
This matrix
![]() is
called orientation matrix or rotation matrix. In complete notation
is
called orientation matrix or rotation matrix. In complete notation
![]() ,
this matrix
,
this matrix
![]() describes
the orientation of frame
describes
the orientation of frame ![]() (and
thereby the body under consideration) with respect to frame
(and
thereby the body under consideration) with respect to frame
![]() .
.
Certainly there is another interpretation possible for the rotation matrix.
Let us consider vector
![]() with
respect to frame
with
respect to frame ![]() ,
which is according to our notation
,
which is according to our notation
![]() .
A reasonable question is how this vector looks like with respect to frame
.
A reasonable question is how this vector looks like with respect to frame
![]() .
It turns out, that the following relation is valid:
.
It turns out, that the following relation is valid:
|
|
(2.4) |
Applying the rotation matrix is therefore an operation to transform vectors
and matrices from one coordinate system to another. The notation in equation
2.4 tells us,
that it is an example where the transformation is from frame
![]() to
frame
to
frame ![]() .
.
Rotation matrices in general have some important attributes, which can be
used for some practical purpose. Given a rotation matrix
![]() in
column vector description:
in
column vector description:
![]()
the following attributes can be proven to be true:
1.)
All column
vectors are scaled to unity:
![]()
2.)
All column vectors are mutually orthogonal:
|
|
|
|
|
|
|
|
|
|
|
|
Because of attributes 1.) and 2.) to be both valid,
![]() is
also called orthonormal.
is
also called orthonormal.
3.)
Because
![]() is
orthonormal, its inverse
is
orthonormal, its inverse
![]() is
equal to its transposed matrix:
is
equal to its transposed matrix:
![]()
A more general notation yield to:
![]()
4.)
The
determinant of the rotation matrix is of value
![]() for
any right-hand cartesian coordinate frame:
for
any right-hand cartesian coordinate frame:
![]()
5.)
The product
![]() of
two orthonormal matrices
of
two orthonormal matrices
![]() ,
,
![]() results
in another orthonormal matrix.
results
in another orthonormal matrix.
6.)
The product of two rotation matrices is non-commutative.
![]() ,
,
, except when either
![]() or
or
![]() is
the identity matrix.
is
the identity matrix.
7.)
Multiplication
of rotation matrices is associative.
![]()
8.)
The
characteristic equation
![]() possesses
one real-valued and two complex-valued solutions for the eigenwert
possesses
one real-valued and two complex-valued solutions for the eigenwert
![]() .
The real eigenwert
.
The real eigenwert ![]() is
of value
is
of value ![]() .
.